————————————————————————————————
Monthly Discussion
One-to-One Substitutions Rarely Are Complete
The mechanism of competitive substitutions was
described in Predictions as a
natural-growth process. The classical example of cars substituting for horses
in the personal transportation market showed how the market shares of horses
and cars followed complimentary S-curves between 100% and 0%, the former going
down and the latter going up, see Exhibit 3.
The Substitution of Cars for Horses
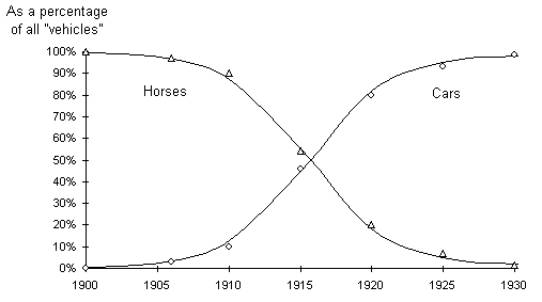
Exhibit
3. The data points represent percentages of
the total number of transportation units, namely, cars plus non-farming horses
and mules. The S-curves are fitted to the data points. The sum of respective
ascending and descending percentages equals 100% at any given time.
Based on the principle that niches in nature do not remain
partially full or partially empty under natural conditions, it is assumed that
one-to-one substitutions proceed to completion, which seems to be the case with
horses and cars. However, if we extend the tie horizon we find that the data
deviates from the natural curves. I Exhibit 4 we see the cars-for-horses
substitution in the logistic transformation that makes S-curves look like
straight lines. It is clear that whereas a perfectly straight line
(intermittent line) describes well the bulk of the substitution process, the
data points after 1930 (black dots) deviate significantly from the
straight-line pattern. This deviation indicates that the number of horses that
did not become substituted is much larger than the natural substitution process
would have forecast.
The Evolution of the Cars’ Market Share with Logistic
Scale
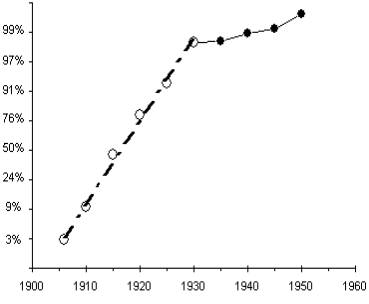
Exhibit 4. The logistic scale of the vertical axis
makes S-curve look like straight lines.
The straight line of the cars’ market share stops in 1930 beyond which
date there are too many horses (black dots).
In the cars-for horses substitution the deviation
from the natural-growth process sets in after the substitution is 98%
completed, therefore the deviation observed has little practical significance,
but more often than not such deviations are much more important.
Exhibit 5 is adapted from the celebrated article by
Fisher and Pry who first suggested that one-to-one substitutions follow
S-curves. I have updated the three substitution processes depicted in this
exhibit with recent data (something not done in Predictions - 10 Years Later).
Deviations from the straight-line patterns appeared
well before the end of the substitution process. For synthetic rubber
substituting natural rubber deviations began around 1980 when the substitution
had reached 76% completion. For synthetic fibers replacing natural fibers
deviations began around 1983 when the substitution had reached 72%, and for
margarine replacing butter deviations began before 1980 when the substitution
had reached 71.5%.
I fact for all three substitution process the final
settling level of substitution seems to be around 2/3 of the total.
Three Celebrated Natural
Substitutions
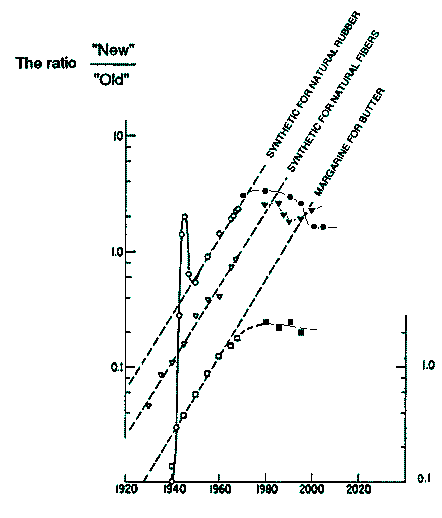
Exhibit
5. The black
data points represent recent data. They generally depict deviations from the
previously established straight-line patterns (S-curves). The
margarine-for-butter substitution (little squares) is graphed on the right
vertical axis. The vertical scales are logarithmic.*
CONCLUSIONS
Contrary
to what may have been expected from the law of natural competition, one-to-one
competitive substitutions do not have to proceed to completion. A “locked” portion of the market share seems
to resist substitution. In three publicized examples of natural substitution
this locked portion was about 1/3 of the market. I have seen even larger such portions. The case of market value
that shifted hands from IBM and Digital Equipment Co. to INTEL and Microsoft
between 1984 and 1994 was a substitution process that proceeded to only 50%.
Competitive substitutions are natural growth
processes and do follow S-curves, but the final ceiling rarely is 100%.
As
disconcerting as it may be when you see a threatening newcomer begin to cutting
persistently into your market share, there is no a priori reason to
interpret his or her gains as a sign of an eventual take-all.