————————————————————————————
Monthly
Discussion
The Halloween Indicator - Revisited
It
is more than three years ago that the Halloween Indicator was discussed in this
newsletter. It is worth perhaps revisiting the subject particularly in view of
the fact that another 5-year period has just been completed. 5-year intervals
were considered in my book An S-Shaped Trail to Wall Street
where I first discussed the subject.
To remind the reader, the concept of
the Halloween Indicator has been introduced by O’Higgins in Beating the Dow.1 It states that that more than 85 percent of annual gains with the
DJIA (just capital gains, not dividends) occur during the winter semester
between October 31 and April 30. In An S-Shaped Trail to Wall Street by
looking at 5-year intervals, I was able to confirm that over a 30-year history
the DJIA gains during winter semesters were effectively the only gains.
Now we have one more 5-year period to take into account.
And the effect persists. Non-fertile
summer semesters have hosted not only stock market crashes, in 1929 and in
1987, but also the 911 catastrophe, if for different reasons. As with the
crashes, the market recovers immediately following the dip—if modestly—until
next April.
Exhibits 3 and 4 show the detailed evolution of
capital returns from the DJIA over the last 35 years. We see both semester
gains and 5-year averages separately for the winter and the summer semesters.
Between October 1968 and October 2003, winter semesters were characterized on
the average by a 9.3% gain, whereas summers by a 1% loss.
Exhibit 3 shows a gentle but steady rise of the
5-year average gains (purple line). Such a rise is practically non-existent in
the summer semesters (Exhibit 4). During the last five years and despite the
much-talked-about bubble, the average gains during winter semesters were 7%
whereas during summer semesters there was an average loss of 3.5%. The
difference between summers and winters was 10.5%, very much in line with the
winter-summer difference of the previous 5‑year intervals.
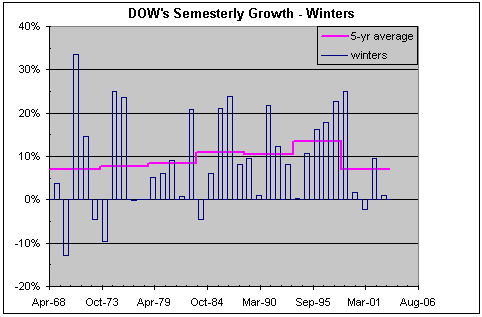
Exhibit 3. The evolution of capital
returns from the DOW during winter semesters, defined as October 31 to April
30, during the last 35 years. The 5-year average (purple line) shows a gently
rising trend.
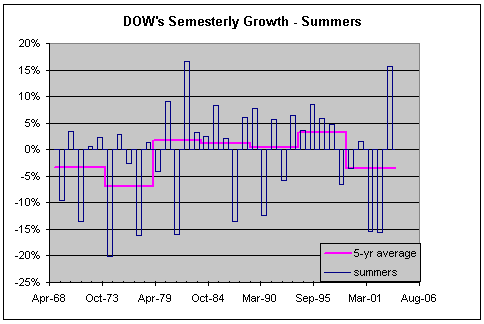
Exhibit 4. The evolution of capital returns from the DOW during summer
semesters, defined as April 30 to October 31, during the last 35 years. The
5-year average (purple line) shows practically no trend.
The fact that the phenomenon of winter-summer
difference persists undaunted indicates that investors have not become aware
of, or simply have not reacted in an important way to this piece of
information. Otherwise the Efficient Market Hypothesis2 would have wiped the phenomenon out. But to the
extent that it still exists, it constitutes an opportunity. Risk-averse
strategies can indeed benefit from portfolios with six-months-on-the-market
six-months-off-the-market strategies.